Value at Risk – Définition, formule et calcul

Qu’est ce que la Value at Risk ?

Dans les banques et les assurances, l’indicateur de risque « Value at Risk » a atteint un statut presque culte depuis le milieu des années 90. Ces dernières années, elle est également de plus en plus utilisée dans d’autres secteurs et domaines de risque. Si l’on traduit littéralement « Value at Risk », on obtient la « valeur à risque » ou le « patrimoine qui est exposé à un risque ». Mais que se cache-t-il exactement derrière cet indicateur ? Dans quelle mesure permet-il d’évaluer correctement un risque ?

Les concepts d’évaluation statistique de la gestion des risques sont multiples : ils vont des simples listes de contrôle aux réseaux neuronaux en passant par la théorie des valeurs extrêmes. Les prestataires de services financiers ont développé au cours des dernières décennies des méthodes statistiques et mathématiques sophistiquées pour calculer les primes en fonction des risques.

De nombreux « ingénieurs financiers » sont toutefois victimes de l’illusion selon laquelle on peut comparer le monde (économique) complexe à une machine. Cette dernière fonctionne selon des chaînes de causes et d’effets claires et qui peut donc également être modélisée à l’aide de certaines équations de comportement interdépendantes. Malgré toutes les erreurs de prévision, le charme d’une déclaration de risque avec un horizon temporel concret, un montant de risque et une probabilité prévaut. C’est dans ce contexte que la Value at Risk s’est développée au cours des dernières années en tant que « mesure standard du risque ».

La naissance de la Value at Risk

Lorsqu’il était président de la banque d’investissement américaine J.P. Morgan, Dennis Weatherstone exigeait chaque jour à 16h15 un rapport de risque d’une page présentant l’exposition totale au marché du portefeuille de négoce de la banque ainsi qu’une estimation des pertes possibles dans les 24 heures suivantes. Weatherstone en avait tout simplement assez que les risques de marché des différents instruments financiers soient mesurés avec des méthodes différentes. Son rapport précédent contenait un nombre incalculable de facteurs bêta et de volatilités, de facteurs de gearing, de deltas, de gammas et de thétas. Il voulait avoir une mesure de risque unique pour tous les instruments financiers.

C’est ainsi qu’est né le « Report 4.15 ». En octobre 1994, J.P. Morgan publie son produit RiskMetrics™ et le met gratuitement à la disposition de toutes les personnes intéressées. Au cœur de ce produit se trouve une méthodologie appelée « Value at Risk ».

Note : La méthode vrio peut également vous intéresser.

Définition et calcul de la Value at Risk

La valeur à risque est définie comme la perte de valeur absolue d’une position à risque définie dans l’entreprise, qui ne sera pas dépassée avec une probabilité définie au préalable (niveau de confiance) au cours d’une période déterminée (période de détention).

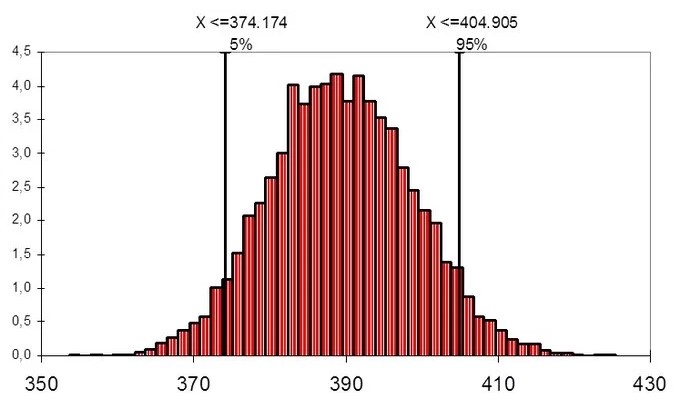
Le graphique suivant présente la valeur à risque. Parmi les actifs simulés, 90 pour cent se situent dans l’intervalle entre 374 174 et 404 905 euros. Cinq pour cent se situent au-dessus ou en dessous. En règle générale, une valeur d’actif encore plus élevée n’est pas considérée comme un risque (« downside risk »), de sorte que les 5 pour cent extrêmement bons sont pris en compte dans la probabilité de ne pas descendre en dessous d’un seuil de perte. Dans l’exemple concret, l’affirmation est la suivante : avec une probabilité de 95 pour cent, l’actif ne sera pas inférieur aux 374 kEUR.

Certaines conditions doivent être remplies pour le calcul de la valeur à risque :

1. Les risques doivent être décomposés en catégories individuelles et décrits à l’aide d’une fonction de distribution appropriée.
2. Les interdépendances entre les risques doivent être connues ou peuvent être estimées.
3. Les caractéristiques des risques doivent être raisonnablement stables et prévisibles dans le temps (les scénarios extrêmes ne sont pas pris en compte).
4. Une base de données fiable doit être disponible.

Pour mesurer la valeur à risque, on peut en principe distinguer deux approches différentes : Une approche analytique et une approche par simulation.

Ces deux approches se distinguent essentiellement sur deux points, à savoir la modélisation de l’évolution des facteurs de risque et la sensibilité des portefeuilles ou des positions considérés. Alors que dans le cadre de l’approche analytique, le modèle est formé sur la base de relations et de rapports connus entre les différentes variables à l’aide d’une hypothèse de répartition, dans l’approche par simulation, la valeur à risque se calcule à partir de la simulation de différentes évolutions d’état.

La simulation historique se base sur des données historiques. Elle suppose que tous les facteurs de risque du passé auront la même influence sur la valeur de la position de risque à l’avenir. La simulation historique est facile à mettre en œuvre en raison de ses faibles exigences mathématiques. Les utilisateurs n’ont pas à se préoccuper de la mesure des volatilités et des corrélations. Ils n’ont pas non plus besoin de connaître le logarithme, la fonction e, la multiplication de matrices ou même la simulation de nombres aléatoires. La simplicité de l’approche est contrebalancée par le fait qu’elle se limite au passé, ce que les critiques comparent souvent au fait de conduire une voiture en regardant dans le rétroviseur. Si la période historique choisie n’est pas représentative de l’avenir, le modèle échoue. De même, il n’est pas possible de simuler des événements qui, bien que possibles, n’ont encore jamais été observés.

La simulation stochastique (voir méthode de Monte-Carlo ou simulation de Monte-Carlo) ne se base pas sur des valeurs historiques, mais sur une variation stochastique des différents paramètres du modèle. Dans le cadre de cette approche stochastique, outre les différentes positions de risque et leurs facteurs d’influence, les corrélations avec d’autres positions de risque sont également prises en compte.

En raison de sa flexibilité, la simulation stochastique est considérée comme supérieure à d’autres méthodes, en particulier pour la mesure des risques d’expositions complexes telles que celles résultant des produits dérivés. La simulation Monte Carlo peut prendre en compte n’importe quelle distribution, les effets de réduction de la durée résiduelle, le clustering de la volatilité, les queues de poisson, les expositions non linéaires et les scénarios extrêmes dans le calcul du risque. Parmi les inconvénients, on peut citer la charge de calcul élevée et la complexité des procédures statistiques utilisées.

En revanche, la méthode analytique présente une complexité similaire selon le cas d’application, mais génère nettement moins de frais de calcul. L’approche dite de variance-covariance présente toutefois l’inconvénient, souvent critiqué, de supposer une distribution normale pour tous les facteurs de risque. Dans la pratique, le modèle de variance-covariance peut servir de première solution rapide, par exemple pour se faire une idée approximative des risques existants actuellement.

Limites de la Value At Risk

Comme toute modélisation, le calcul de la valeur à risque est un exercice d’équilibre entre complexité et précision. Ainsi, les concepts d’évaluation analytique se basent sur des risques individuels normalement distribués, car les modèles qui en résultent seraient sinon trop complexes et donc ingérables. Des compromis similaires doivent être faits avec les méthodes de simulation historique et de Monte Carlo. Certes, on y renonce généralement à l’hypothèse de la distribution normale, mais, par nature, seule une sélection finie du nombre infini d’évolutions et de conditions environnementales possibles peut être prise en compte. D’une part, ces simplifications et restrictions constituent une condition nécessaire pour pouvoir effectuer le calcul. D’autre part, elles entraînent également des imprécisions, car le modèle doit toujours rester incomplet.

Outre ces déficits méthodologiques, dont il faut inévitablement s’accommoder, l’interprétation économique de l’indicateur Value at Risk est également souvent critiquée. Le résultat des calculs est une valeur qui ne sera pas dépassée avec une probabilité définie de 95 pour cent par exemple. Une telle définition ne tient toutefois pas compte des valeurs de risque dont la probabilité est supérieure à 95 ou 100 pour cent. Si l’on augmentait le niveau de confiance à 99,5 pour cent, un plus grand nombre de scénarios pourraient être représentés, mais une valeur résiduelle inconnue avec une très faible probabilité d’occurrence serait également conservée (0,5 pour cent). Formulé de manière générale, le percentile β peut également être interprété comme un événement de 200 ans. Dans le cas d’un événement de 200 ans, il s’agit d’un sinistre qui survient en moyenne tous les 200 ans.

Aucune indication n’est donnée sur la périodicité, c’est-à-dire que le sinistre ne doit pas se produire à des intervalles de 200 ans. Il peut aussi se produire par exemple cinq fois de suite, puis plus pendant longtemps, et l’hypothèse du modèle était malgré tout correcte. De même, l’affirmation de la probabilité est assortie d’une probabilité d’erreur propre, de sorte que dans un backtesting du modèle, des observations s’écartant de la probabilité dans des fourchettes calculées vers le bas et vers le haut sont autorisées sans que le modèle puisse être rejeté.